Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны соответствующим сторонам другого.
 A =
A =  A1,
A1,  B =
B =  B1,
B1,  С =
С =  С1,
С1,
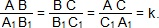
Теорема 1
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
1 уровень
Упражнения 1, 3 стр. 73
2 уровень
Упражнения 2, 4 стр. 73
3 уровень
Упражнение 5 стр. 73, упражнение 33 стр. 76
4 уровень
Упражнение 8 стр. 73, упражнение 34 стр. 76, упражнение 101 стр. 83
Другими словами, два треугольника подобны, если их можно обозначить буквами ABC и A1B1C1 так, что
 A =
A =  A1,
A1,  B =
B =  B1,
B1,  С =
С =  С1,
С1,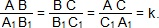
Число k, равное отношению сходственных сторон треугольника называется коэффициентом подобия.
Подобие треугольников ABC и A1B1C1 обозначается:
∆ ABC ~ ∆ A1B1C1. На рисунке 1 изображены подобные треугольники.
Теорема 1
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Теорема 2
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Домашнее задание
глава 3, параграф 1
Задания находятся в книге В.В. Казакова "Наглядная геометрия. Опорные конспекты. Контрольные вопросы. Задачи на готовых чертежах. 8 класс"
1 уровень
Упражнения 1, 3 стр. 73
2 уровень
Упражнения 2, 4 стр. 73
3 уровень
Упражнение 5 стр. 73, упражнение 33 стр. 76
4 уровень
Упражнение 8 стр. 73, упражнение 34 стр. 76, упражнение 101 стр. 83



Комментариев нет:
Отправить комментарий